経路積分に現れる演算子の足跡 ーOrderingについて
$$\def\bra#1{\mathinner{\left\langle{#1}\right|}}$$ $$\def\ket#1{\mathinner{\left|{#1}\right\rangle}}$$$$\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}$$
前回の記事に経路積分量子化を用いると量子力学を扱っているにも関わらず演算子がexplicitに現れないということを話した。
今回はそのことについてもう少し正確に、詳しく話していく。
まず普通に正準量子化で考えたときに、量子力学と古典力学は古典極限\(\hbar\to0\)のもとで1:1対応をしていない。
例えばHamiltonianを古典的に$$H=pq$$という形で考えてみよう。
位置演算子\(\hat{Q}\)と運動量演算子\(\hat{P}\)は古典極限\(\hbar\to0\)のもとでc-数に帰着するのでこの古典的Hamiltonianに対応する量子Hamiltonianは$$\hat{H}=\hat{P}\hat{Q}$$という形で考えればこの量子系は古典極限のもとで無事元の古典系に帰着するようになる。
しかしこの古典系に帰着できる量子系のHamiltonianはこれだけではない。実際に$$\hat{H}=\hat{Q}\hat{P},~~~~\hat{H}=\frac{1}{2}\left(\hat{P}\hat{Q}+\hat{Q}\hat{P}\right)\cdots$$も上の量子Hamiltonianとは異なるがこれも同じ古典系に帰着できる。
つまり一般的には演算子は非可換性を持っているために古典Hamiltonianの下で量子Hamiltonianは演算子の並べ方の分だけ不定性が存在する。
そのため通常量子力学を考えるときはある特定の演算子の順序(Ordering)をとり考える。
これを踏まえた上で古典力学\(H\left(x,p\right)\)に対応する「量子系のうち運動量演算子がいつも左側にくるOrdering」を考えよう。
このようなOrderingをNormal Ordering(正規順序)と呼ぶ。
Normal Orderingの量子Hamiltonianを\(\hat{H}_{N.O.}\)と書くことにするとこのOrderingでのHamiltonianのmatrix elementはこのHamiltonianの表式の中にはいつも運動量演算子が左側にくるので運動量の完全系を次のように挿入すると$$\begin{align}\bra{x’}\hat{H}_{N.O.}\left(\hat{P},\hat{Q}\right)\ket{x}&=\int dp\braket{x’}{p}\bra{p}\hat{H}_{N.O.}\left(\hat{P},\hat{Q}\right)\ket{x}\\ &=\int \frac{dp}{2\pi\hbar}e^{\frac{i}{\hbar}p\left(x’-x\right)}H(p,x)\tag{1}\end{align}$$となる。
Fourier係数をみてみると量子Hamiltonianに対して\(\hat{Q}\to q,~~\hat{P}\to p\)の置き換えをしたものになっている。
これがNormal Orderingでの結果であるが、また別のOrderingを考えてみよう。
Normal Orderingと同じくらいによく使われるOrderingがWeyl Orderingである。
これは「考えうる順序を全て同じweightで足したOrdering」である。
古典極限をとると各項の演算子の順序はもはや関係なくなってしまい項数の分だけ古典Hamiltonianが得られる。そこでweigtとして項数で全体を割ってあげれば古典極限で得られるHamiltonianは元の古典Hamiltonianに完全に帰着できる。
まさに上で挙げた量子Hamiltonianの3つ目がそれに該当する。この場合は2項だけでよかったが例えば古典Hamiltonianを\(qpq\)とすると演算子の考えうる順序は$$\hat{Q}^2\hat{P},~~\hat{Q}\hat{P}\hat{Q},~~\hat{P}\hat{Q}^2~~\left(\hat{P}が左にずれてくイメージ\right)$$の3通り。この全てが古典極限のもとで\(qpq\)に帰着してしまうのでWeyl Orderingを考える、と言った時には$$\hat{H}_{W.O.}=\frac{1}{3}\left(\hat{Q}^2\hat{P}+\hat{Q}\hat{P}\hat{Q}+\hat{P}\hat{Q}^2\right)$$とすれば良い。
さらに一般的な\(q^np^m\)のような場合を考えてみよう。\(n+m\equiv N\)とすると\(n\)個の\(\hat{Q}\)と\(m\)個の\(\hat{P}\)の組み合わせから得られる\(N\)個のHamiltonianのうち\(n\)個は\(\hat{Q}\)により、また\(m\)個は\(\hat{P}\)によりsymetricになるので最終的に独立な演算子の並べ方は\(\frac{N!}{n!m!}\)である。なのでweight\(\frac{N!}{n!m!}\)で組み合わせの和全体を割ってあげるとこれがWeyl Orderingになる:$$\hat{H}_{W.O.}=\frac{n!m!}{N!}\sum_{All combination}\left(\hat{Q}^n\hat{P}^m\right)\equiv\left(\hat{Q}^n\hat{P}^m\right)_{W.O.}$$ではこれをもとに一般的な多項式\(\left(\alpha\hat{Q}+\beta\hat{P}\right)^N\)を展開してみよう。
naiveに展開していくと$$\begin{align}\left(\alpha\hat{Q}+\beta\hat{P}\right)^N &=\alpha^N\hat{Q}^N\\&+\alpha^{N-1}\beta\left(\hat{Q}^{N-1}\hat{P}+\hat{Q}^{N-2}\hat{P}\hat{Q}+\cdots+\hat{P}\hat{Q}^{N-1}\right)\\ &+\alpha^{N-2}\beta^2\left(\hat{Q}^{N-2}\hat{P}^2+\hat{Q}^{N-3}\hat{P}\hat{Q}\hat{P}+\cdots\right)\\ &+\cdots\\ &=\sum_{l=0}^{N}\alpha^{N-l}\beta^l\left(\hat{Q}^{N-l}\hat{P}^l\right)_{W.O.}\frac{N!}{(N-l)!l!}=\sum_{n+m=N}\frac{N!}{n!m!}\alpha^n\beta^m\left(\hat{Q}^n\hat{P}^m\right)_{W.O.}\end{align}$$とできる。
一つ目の等式では各項に現れる演算子の和は各\(n,m\)の値でのWeyl Orderingになっている:$$\begin{align}&\hat{Q}^{N-1}\hat{P}+\hat{Q}^{N-2}\hat{P}\hat{Q}+\cdots+\hat{P}\hat{Q}^{N-1}=\left(\hat{Q}^{N-1}\hat{P}\right)_{W.O.}\times\frac{N!}{(N-1)!1!}\\ &\hat{Q}^{N-2}\hat{P}^2+\hat{Q}^{N-3}\hat{P}\hat{Q}\hat{P}+\cdots=\left(\hat{Q}^{N-2}\hat{P}^2\right)_{W.O.}\times\frac{N!}{(N-2)!2!}\end{align}$$これがわかると指数関数\(e^{\alpha\hat{Q}+\beta\hat{P}}\)は展開するとまさにこの多項式が現れるのでこの指数関数自体をWeyl Orderingで表示できるようになる:$$\begin{align}e^{\alpha\hat{Q}+\beta\hat{P}}&=\sum_{l=0}^\infty\frac{1}{l!}\left(\alpha\hat{Q}+\beta\hat{P}\right)^l\\ &=\sum_{l=0}^\infty\sum_{n+m=l}\frac{1}{l!}\frac{l!}{n!m!}\alpha^n\beta^m\left(\hat{Q}^n\hat{P}^m\right)_{W.O.}\end{align}$$このようにするとHamiltonianが一般的でより複雑なWeyl Orderingの多項式の場合、この指数関数の形であわらすことができる。また指数形であるため次のようにCampbell-Baker-Hausdorffの公式を使うことができる:$$\begin{align}e^{\frac{\alpha\hat{Q}}{2}}e^{\beta\hat{P}}e^{\frac{\alpha\hat{Q}}{2}}&=e^{\frac{\alpha\hat{Q}}{2}}e^{\beta\hat{P}+\frac{\alpha}{2}\hat{Q}+\frac{1}{2}\alpha\beta[\hat{P},\hat{Q}]+\cdots}\\ &\sim e^{\frac{\alpha\hat{Q}}{2}}e^{\beta\hat{P}+\frac{\alpha}{2}\hat{Q}-\frac{i\hbar}{4}\alpha\beta}\\ &\sim e^{\frac{\alpha\hat{Q}}{2}+\beta\hat{P}+\frac{\alpha\hat{Q}}{2}-\frac{i\hbar}{4}\alpha\beta+\frac{1}{2}\alpha\beta[\hat{Q},\hat{P}]+\cdots}\\ &\sim e^{\alpha\hat{Q}+\beta\hat{P}}\end{align}$$つまり一般的なWeyl OrderingのHamiltonian\(e^{\alpha\hat{Q}+\beta\hat{P}}\)のmatrix elementを考えるときこの関係を使うことができる。$$\begin{align}\bra{x’}\hat{H}_{W.O.}\left(\hat{Q},\hat{P}\right)\ket{x}=\bra{x’}e^{\alpha\hat{Q}+\beta\hat{P}}\ket{x}&=\bra{x’}e^{\frac{\alpha\hat{Q}}{2}}e^{\beta\hat{P}}e^{\frac{\alpha\hat{Q}}{2}}\ket{x}\\ &=e^{\frac{\alpha x’}{2}}\bra{x’}e^{\beta\hat{P}}\ket{x}e^{\frac{\alpha x}{2}}\\ &=\int dp e^{\frac{\alpha x’}{2}}\bra{x’}e^{\beta\hat{P}}\ket{p}\braket{p}{x}e^{\frac{\alpha x}{2}}\\ &=\int \frac{dp}{2\pi\hbar}e^{\frac{\alpha}{2}(x+x’)+\beta p}e^{\frac{i}{\hbar}p(x-x’)}=\int \frac{dp}{2\pi\hbar}H\left(\frac{x+x’}{2},p\right)e^{\frac{i}{\hbar}p(x-x’)}\tag{2}\end{align}$$Fourier係数をみてみると量子Hamiltonianの引数\(\hat{Q}\)が\(x\)と\(x’\)の中点\(\frac{x+x’}{2}\)に置き換えられていることがわかる。
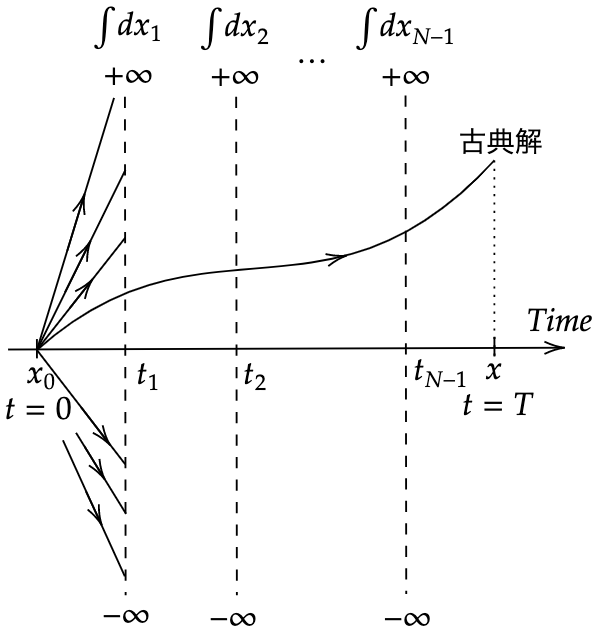
ここまでわかるとようやく経路積分(Feynman核)にこのOrderingの内容を反映させることができる。
実際Feynman核は経路積分の形に持っていく時に各時刻で位置の完全系を挿入していく(詳しくはコチラ)いき、\(\braket{t_j,x_j}{t_{j-1},x_{j-1}}\)を計算しなければいけない。
これを書き換えると$$\begin{align}\braket{t_j,x_j}{t_{j-1},x_{j-1}}&=\bra{x_j}e^{-\frac{i}{\hbar}\hat{H}t_j}e^{+\frac{i}{\hbar}\hat{H}t_{j-1}}\ket{x_{j-1}}\\ &=\bra{x_j}e^{-\frac{i}{\hbar}\left(t_j-t_{j-1}\right)\hat{H}}\ket{x_{j-1}}\end{align}$$となる。この表式のなかに現れる\(\hat{H}\)にOrderingを反映するのだが、Normal Orderingの時のmatrix elementは(1)式、Weyl Orderingの時のmatrix elementは(2)式を用いれば良い。
ここではWeyl Orderingを採用することにすると$$\int \frac{dp_j}{2\pi\hbar}e^{\frac{i}{\hbar}p_j\left(x_j-x_{j-1}\right)-\frac{i}{\hbar}\left(t_j-t_{j-1}\right)H\left(\frac{x_j+x_{j-1}}{2}~,~p_j\right)}$$経路積分を紹介した記事ではHamiltonianを運動量のQuadraticな形に具体化して考えていたが、より一般的なHamiltonianを考える際にはこのようにOrderingをとって考えれば良い。
一方ここでNormal Orderingを考えると\(H\)の引数はWeyl Orderingと違くなってしまう。
しかし経路積分として時間間隔と格子数の極限\(\epsilon\to0,N\to\infty\)をとるとindex jのカウントはもはや違いを産まず結局経路積分の表式に現れるのはどちらのOrderingをとっても\(H(x,p)\)に帰着するので心配はない(各Orderingは1つの古典Hamiltonianに帰着するはずなので当然)。
経路積分を考えると結局は作用\(S[x]\)を考えれば良いので演算子がexplicitには現れないが、そこに至るまでの過程には当然演算子は(Hamiltonianの中に)姿を表しており、これらはOrderingとして現れている。
投稿者プロフィール

-
素粒子物理学を研究しています。
物理学を「面白い学問」で終わらせないこと、そこから「人生のなかで核心となる精神」を学んで生きることが僕の哲学です。
最新の投稿
 日々思うこと2021年3月17日鄭 明析牧師の名説教:「愛の電気」
日々思うこと2021年3月17日鄭 明析牧師の名説教:「愛の電気」 日々思うこと2021年2月21日しばらくM1 mac book proを使ってみて思ったこと
日々思うこと2021年2月21日しばらくM1 mac book proを使ってみて思ったこと 日々思うこと2021年2月20日「対称性の破れ」からみる神様の性格
日々思うこと2021年2月20日「対称性の破れ」からみる神様の性格 日々思うこと2020年8月31日光のDoppler効果 ー高校生のときの思い出ー
日々思うこと2020年8月31日光のDoppler効果 ー高校生のときの思い出ー

