汎関数って結局なに？

解析力学に始まり量子力学、場の量子論をやっていると汎関数というものが出てくる。
その振る舞いはほとんど普通の関数と変わらないし、汎関数用の微分ー汎関数微分も普通の微分とその感覚は全く変わらない。
でも結局汎関数ってなに？　というのを整理してみよう。

まず、関数というのはみんなよく知っているようにある変数(の組)に対して1:1で値を返すような写像を関数と呼ぶ。
例えばLagrangianというのは $$\mathscr{L}\left(x(t),\dot{x}(t)\right)=\frac{1}{2}m\left(\dot{x}(t)\right)^2-V\left(x(t)\right)$$ という形をしているが、この場合時間$t$をパラメータとして粒子の軌跡$x(t)$は時間の関数であり、さらにLagrangianはこの軌跡(とその時間微分)の合成関数になっている。
一方で作用は $$S[x]=\int_{t_i}^{t_f}dt L\left(x(t),\dot{x}(t)\right)$$ で定義されるが、注意すべきは作用はLagrangianや粒子の軌跡見たいな変数との1:1対応を持つ合成関数ではないということである。
なぜなら$t$の値を1つ固定するとその関数である粒子の軌跡及びLagrangianは1:1でuniqueに決まる。
しかし作用は$t$の値を$[t_i,t_f]$の区間で積分をした結果1つの値を返す。言うなれば作用は時間$t$に対して$\infty$:1対応をした無限変数関数である。
言い換えると$[t_i,t_f]$までの粒子の軌跡を1本決めると作用の値が1つにきまる。
このような(関数全体＝$\infty$個の値)$\to$(値)の対応を持つ写像を汎関数と呼んでいる。一般に汎関数であることを明示するためにその引数は丸括弧()ではなく角括弧[]で囲む。

より数学的に一般の形で汎関数をかくと $$F[f]\equiv\int dx\mathscr{F}\left(f(x)\right)$$ になる。汎関数の微分ー汎関数微分を次に考えよう。
普通の微分の場合は変数を微小に動かすことに伴う関数の変化量をみるが、これに習って今の場合はintegrand$\mathscr{F}$の引数になっている$f(x)$を微小に変化させる。つまり$f(x)$の関数形を微小に変えて、それに伴う汎関数の変化量をみるという処理を汎関数微分と定義する： $$\frac{\delta F\left(f\right)}{\delta f(y)}\equiv\lim_{\epsilon\to0}\frac{\int dx \mathscr{F}\left(f(x)+\epsilon\delta(x-y)\right)-\int dx\mathscr{F}\left(f(x)\right)}{\epsilon}\tag{1}$$ ここで$x=y$で関数形を微小に($\epsilon$だけ)変化させることを考えているがそれ以外の点では変化しないことを反映させるために微小量$\epsilon$のあとに$\delta$関数をつけている。
注意すべきはこの汎関数微分は無限個ある汎関数の変数$x$のうち1点だけでの微分を考えていることになる。いわばその点に関する偏微分を考えているようなもので、全体の点での微分を合わせた全微分のようなものも考えることができる。
2変数とかそういう有限個の変数を持つ関数の場合には$\sum$記号だったものが今はビッシリ詰まった無限個の変数を持っているので$\int$におきかわる： $$\frac{d}{d\epsilon}F[f+\epsilon v]|_{\epsilon=0}=\int dx\frac{\delta F[f]}{\delta f(x)}v(x)\tag{2}$$ これが$x$の定義域全体で関数$f$の形を変えた時の汎関数の変化率になる。

(1)式の分子に注目すると乗っかってるのは単にintegrandの差になっているのでこれは $$\mathscr{F}\left(f(x)+\epsilon\delta(x-y)\right)-\mathscr{F}\left(f(x)\right)=\frac{\partial\mathscr{F}\left(f(x)\right)}{\partial f(x)}\epsilon\delta(x-y)+\mathscr{O}\left(\epsilon^2\right)$$ のようにできる。これを(1)式に代入すると $$\frac{\delta\mathscr{F}\left(f(x)\right)}{\delta f(y)}=\frac{\partial\mathscr{F}\left(f(x)\right)}{\partial f(x)}\delta(x-y)$$ とできる。これで汎関数微分$\frac{\delta}{\delta f(x)}$と普通の微分$\frac{\partial}{\partial f(x)}$を結ぶ式が得られた。
さらにこれの両辺を積分すると $$\int dx \frac{\delta\mathscr{F}\left(f(x)\right)}{\delta f(y)}=\frac{\delta F[f]}{\delta f(x)}=\int dx \frac{\partial\mathscr{F}\left(f(x)\right)}{\partial f(x)}\delta(x-y)=\frac{\partial\mathscr{F}\left(f(y)\right)}{\partial f(y)}$$ を得る。整理すると $$\frac{\delta F[f]}{\delta f(x)}=\frac{\partial\mathscr{F}\left(f(x)\right)}{\partial f(x)}$$ となり、汎関数(偏)微分はintegrandの微分に等価であることがわかった。
これがわかるとintegrandが関数$f(x)$そのものである、つまり合成関数$\mathscr{F}$は恒等写像である時、 $$\frac{\delta f(x)}{\delta f(y)}=\frac{\partial f(x)}{\partial f(x)}\delta(x-y)=\delta(x-y)$$ であることがわかる。

これくらいがわかっていれば最低限物理の中で自由に汎関数を使いこなせると思う。
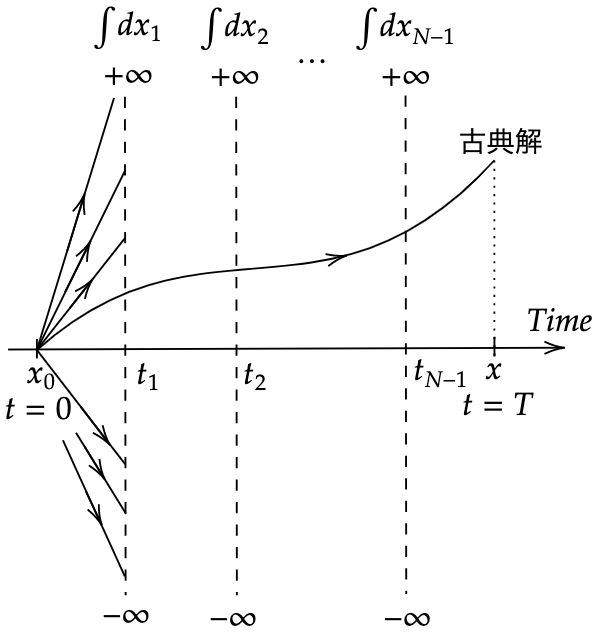
例えば経路積分を例にとって考えてみると系の経路積分を評価するためには作用$S[x]$を考えなければいけない。
ここで粒子の量子力学的な軌跡$x(t)$を古典解$x_c(t)$とその周りでの揺らぎ$\eta(t)$に分解してみよう：$x(t)=x_c(t)+\eta(t)$
もともと大きい揺らぎを持つ経路は積分に寄与してこない(詳しくは経路積分のページで)ので、古典解近傍での微小な揺らぎだけを考えれば良い。なので結局は作用$S[x_c+\eta]$は$\eta$のベキで展開できるようになり、 $$S[x]=S[x_c]+\int dt \frac{\delta S[x]}{\delta x(t)}|_{x=x_c}\eta(t)+\frac{1}{2!}\int dt_1dt_2\frac{\delta^2S[x]}{\delta x(t_1)\delta x(t_2)}|_{x=x_c}\eta\left(t_1\right)\eta\left(t_2\right)+\cdots$$ これを計算していくわけだが、2項目はEuler-Lagrange方程式により落とすことができるので3項目の2階汎関数微分から計算していけば良い。
とは言ってもより一般的な系($x$の3次以上のポテンシャルを含んだ系)でない限り、例えば調和振動子を考えるとLagrangianに含まれてる$x$の数は高々2個なので2回汎関数微分を作用させると全ての項はただの$\delta$関数を含む項になってしまってそれより高次の項は全て消えてしまう。
なので実質調和振動子の場合はこの2階汎関数微分だけを計算できればいい。実際計算するにはstraightforwardにも計算できる。
ただもう1つの方法を紹介しておくとあくまでもここで計算しているのは2階の汎関数偏微分だと思うとこれは汎関数全微分((2)式)の中の2次の係数だとわかる。なのでまずは(2)式で考えた汎関数全微分を計算してその2次の係数を取り出す、という方法もできる。
双方が同じ結果を出すことは各自で確かめてもらえたらと思う。

道具として使っていてもなかなか汎関数が掴めないという点が少しでも整理されたと願いたい・・・！

投稿者プロフィール

素粒子兄弟

素粒子物理学を研究しています。
物理学を「面白い学問」で終わらせないこと、そこから「人生のなかで核心となる精神」を学んで生きることが僕の哲学です。

最新の投稿

• 日々思うこと2021年3月17日鄭 明析牧師の名説教：「愛の電気」
• 日々思うこと2021年2月21日しばらくM1 mac book proを使ってみて思ったこと
• 日々思うこと2021年2月20日「対称性の破れ」からみる神様の性格
• 日々思うこと2020年8月31日光のDoppler効果　ー高校生のときの思い出ー