Feynmanダイアグラムを描いてみた(経路積分) ーPart5ー

日々思うこと

$$\def\bra#1{\mathinner{\left\langle{#1}\right|}}$$ $$\def\ket#1{\mathinner{\left|{#1}\right\rangle}}$$ $$\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}$$

☆前回までのキーワード：自由粒子のFeynman核

前回次回予告でn点関数を計算すると書いたが、今日は番外編(気分屋なので許してくださいρ(~~))。Feynman核から経路積分というものを導入する。そもそも普通量子力学は正準量子化(物理量が数から演算子として非可換な世界に置き換わる)によって導入される理論であるが、ここ最近では正準量子化よりもこの経路積分を量子化のformalismとしていきなり採用して量子力学の講義をしている大学があるらしい。実際後で見るようにこの経路積分の考え方はとても直観的に納得しやすいものであるためそうなるのもうなずける。では早速ウワサの経路積分をみてみよう。

まずFeynman核の形をみてみると時間発展演算子$U(t,t_0)=e^{-\frac{i}{\hbar}\hat{H}(t-t_0)}$が基底$\bra{x}$と$\ket{x_0}$にsandwitchされているが、この時間発展演算子を$[t_0,t]=[0,T]$の区間の中で$N$等分することが可能である(下図を参照)。つまり$$\begin{align}K(x,x_0;T)&=\bra{x}U(T,t_{N-1})\cdots U(t_1,0)\ket{x_0}\\ &=\bra{x}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{N-1})\Delta t\right)\cdots\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_0)\Delta t\right)\ket{x_0}\end{align}$$とすることができる。もちろん最初の時間発展演算子$U(T,0)$は微小な時間発展$\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t)\Delta t$を連続的に繰り返して得られるものであるから最後に$N\to\infty$の極限を取るべきである。

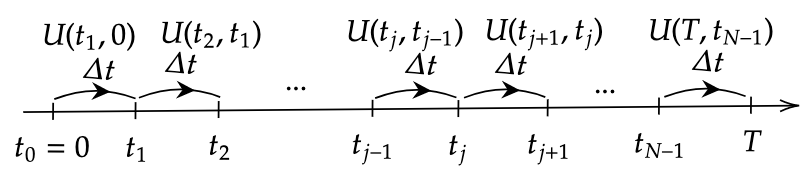
次に区間$[0,T]$を$N$等分した各時刻$t_1\cdots t_{N-1}$に座標の完全系を挿入する。$$\begin{align}K(x,x_0;T)&=\bra{x}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{N-1})\Delta t\right)\int dx_{N-1}\ket{x_{N-1}}\bra{x_{N-1}}\cdots\int dx_{1}\ket{x_1}\bra{x_1}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{0})\Delta t\right)\ket{x_0}\\ &=\int dx_{N-1}\cdots dx_1 \bra{x}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{N-1})\Delta t\right)\ket{x_{N-1}}\cdots\bra{x_j}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{j-1})\Delta t\right)\ket{x_{j-1}}\cdots\bra{x_1}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{0})\Delta t\right)\ket{x_0}\\ &=\int dx_{N-1}\cdots dx_1 K(x,x_{N-1};T,t_{N-1})\cdots K(x_{j},x_{j-1};t_j,t_{j-1})\cdots K(x_1,x_0;t_1,0)\\ &=\prod_{j=1}^{N-1}\int dx_j \prod_{j=1}^{N}K(x_j,x_{j-1};t_j,t_{j-1})\tag{1}\quad(x_N\equiv x,t_N\equiv T)\end{align}$$このように全体のFeynman核は微小時間でのFeynman核の”積み重ね”で表される。続けてHamiltonianが運動量に関してQuadratic($2$次)で表される場合すなわち$$\hat{H}(t)=\frac{1}{2m}\hat{P}^2+V(t,\hat{Q})$$で表されるときに(1)式が具体的にどのような形になるかを見ていく。微小時間でのFeynman核は$$\begin{align}K(x_j,x_{j-1};t_j,t_{j-1})&=\bra{x_j}\left(\boldsymbol{1}-\frac{i}{\hbar}\hat{H}(t_{j-1})\Delta t\right)\ket{x_{j-1}}\\ &=\bra{x_j}\left(\boldsymbol{1}-\frac{i}{\hbar}\left(\frac{1}{2m}\hat{P}^2+V(t_{j-1},\hat{Q})\right)\Delta t\right)\ket{x_{j-1}}\end{align}$$ここで今度は座標と同じindexを持つ運動量の完全系を挿入すると$$K(x_j,x_{j-1};t_j,t_{j-1})=\bra{x_j}\int dp_j\ket{p_j}\bra{p_j}\left(\boldsymbol{1}-\frac{i}{\hbar}\left(\frac{1}{2m}\hat{P}^2+V(t_{j-1},\hat{Q})\right)\Delta t\right)\ket{x_{j-1}}$$となるが、$\hat{P}$は$\bra{p_j}$に作用する一方で$\hat{Q}$は$\ket{x_{j-1}}$に作用して時間発展演算子はc-数となる。$$K(x_j,x_{j-1};t_j,t_{j-1})=\frac{1}{2\pi\hbar}\int dp_j exp\left(\frac{i}{\hbar}p_j(x_j-x_{j-1})\right)\left(1-\frac{i}{\hbar}\left(\frac{1}{2m}p_j^2+V(t_{j-1},x_{j-1})\right)\Delta t\right)$$また$N\to\infty$の極限の下で$\Delta t\ll 1$になるので$$\lim_{N\to\infty}K(x_j,x_{j-1};t_j,t_{j-1})=\frac{1}{2\pi\hbar}\int dp_j exp\left(\frac{i}{\hbar}\left(p_j\frac{(x_j-x_{j-1})}{\Delta t}-\frac{1}{2m}p_j^2-V(t_{j-1},x_{j-1})\right)\Delta t\right)$$次に上式の運動量積分は平方完成をした上でGauss積分として計算できる(この計算は自由粒子Feynman核の計算でも出てきた)。$$\begin{align}\lim_{N\to\infty}K(x_j,x_{j-1};t_j,t_{j-1})&=\frac{1}{2\pi\hbar}exp\left(\frac{i}{\hbar}\left(\left(\frac{m(x_j-x_{j-1})^2}{2\Delta t^2}\right)-V(t_{j-1},x_{j-1})\right)\Delta t\right)\int dp_j exp\left(\frac{i\Delta t}{2m\hbar}\left(p_j-\frac{m(x_j-x_{j-1})}{\Delta t}\right)^2\right)\\ &=\frac{1}{2\pi\hbar}\sqrt{\frac{2m\hbar\pi}{i\Delta t}}exp\left(\frac{i}{\hbar}\left(\left(\frac{m(x_j-x_{j-1})^2}{2\Delta t^2}\right)-V(t_{j-1},x_{j-1})\right)\Delta t\right)\\ &=\sqrt{\frac{m}{2i\hbar\pi\Delta t}}exp\left(\frac{i}{\hbar}\left(\left(\frac{m(x_j-x_{j-1})^2}{2\Delta t^2}\right)-V(t_{j-1},x_{j-1})\right)\Delta t\right)\tag{2}\end{align}$$これを全体のFeynman核(1)式に代入すると$$K(x,x_0;T)=\lim_{N\to\infty}\left(\prod_{j=1}^{N-1}\sqrt{\frac{m}{2i\hbar\pi\Delta t}}\int dx_j\right)\sqrt{\frac{m}{2i\hbar\pi\Delta t}}\prod_{j=1}^{N}exp\left(\frac{i}{\hbar}\left(\left(\frac{m(x_j-x_{j-1})^2}{2\Delta t^2}\right)-V(t_{j-1},x_{j-1})\right)\Delta t\right)$$となる。ここで係数$\sqrt{\frac{m}{2i\hbar\pi\Delta t}}$は(2)式を代入した時点では$N$個あるが一つ目の$\Pi$は$N-1$までしかCountしないのでその外に残りの1個を出している。また2つ目の$\Pi$で指数関数の積をとっているがこれは位相部分で和をとった指数関数に等しいので$$K(x,x_0;T)=\lim_{N\to\infty}\sqrt{\frac{m}{2i\hbar\pi\Delta t}}\left(\prod_{j=1}^{N-1}\sqrt{\frac{m}{2i\hbar\pi\Delta t}}\int dx_j\right)exp\left(\frac{i}{\hbar}\sum_{j=1}^{N}\Delta t\left(\frac{m}{2}\left(\frac{x_j-x_{j-1}}{\Delta t}\right)^2-V(t_{j-1},x_{j-1})\right)\right)$$位相部分を見てみると$\frac{x_j-x_{j-1}}{\Delta t}$は$[x_0,x]$の区間内で$\Delta t$で区切られた微小時間での微分を与え、$j=1\sim j=N$での和はそれを$(x_0,t_0=0)$から$N$回繰り返すという事であるから$[0,T]$での時間積分を与える。また積分測度の部分を$$\mathscr{D}x\equiv\lim_{N\to\infty}\sqrt{\frac{m}{2i\hbar\pi\Delta t}}\left(\prod_{j=1}^{N-1}\sqrt{\frac{m}{2i\hbar\pi\Delta t}}\int dx_j\right)$$と定義すると結局$$K(x,x_0;T)=\int\mathscr{D}x e^{\frac{i}{\hbar}S[x]}\tag{3}\\ \left(S[x]\equiv\int_{0}^{T}dt\left(\frac{1}{2}m\dot{x}(t)^2-V(t,x(t))\right)\right)$$となる。この(3)式をFeynman核の経路積分表示と呼ぶ。また$S[x]$は始状態と終状態とを結ぶ経路$x(t)$と1:1で対応している汎関数である。言い換えると各経路にはweight$e^{\frac{i}{\hbar}S}$がassignされており、このweightで各経路を足しあげたものが経路積分とも言える。

(3)式がどうして経路積分と呼ばれているのかについて最後に見てみよう。
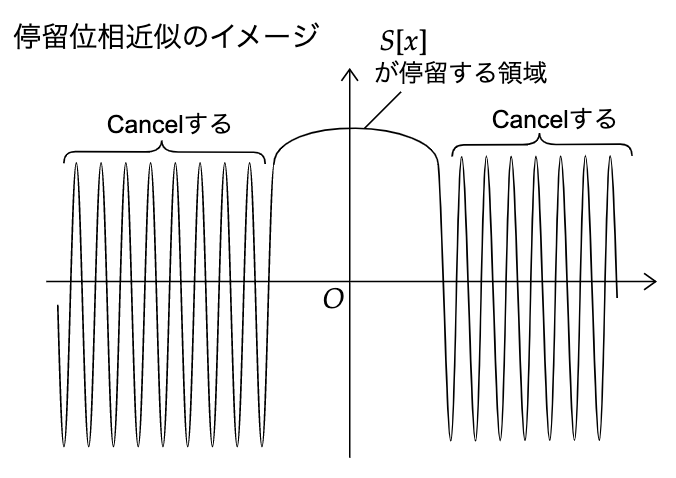
weight$e^{\frac{i}{\hbar}S}$(の実部または虚部)は$\mathscr{O}(\hbar)$で振動をする。そのため古典極限$\hbar\to 0$または$\hbar\ll |S[x]|$のもとで振動は激しくなり$\pm 1$の間を激しく振動、つまり$S$の値が微小に変わるだけでweightの符号が簡単に反転してしまう。
このような経路どうしは積分をとると互いにCancelしてしまい全体の結果に寄与するのは$S[x]$の値が停留する部分(=古典解とその近傍)のみになる(下図を参照。縦軸はweight$e^{\frac{i}{\hbar}S}$、横軸は作用$S$として正確ではないもののそのイメージを示した。この近似は停留位相近似と呼ばれしばしば場の理論をやっているとでてくる。証明はここでは省略させてください/(_ _)/)。

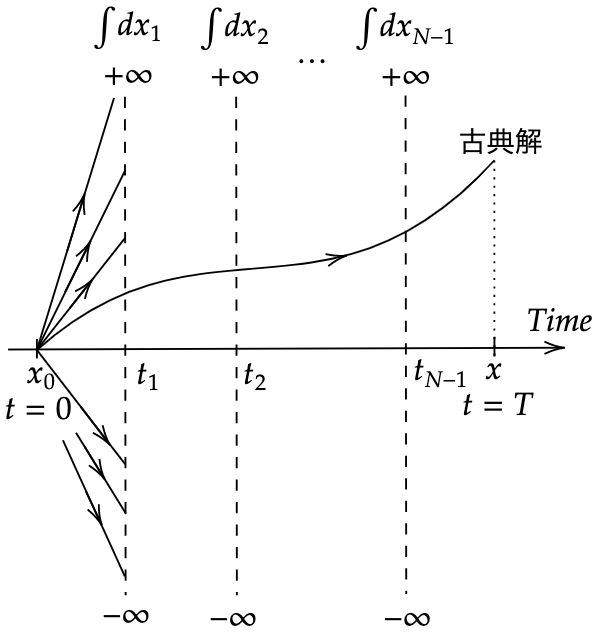
作用が停留するというのは作用原理と同じなので結局この古典極限の下でEuler-Lagrange方程式(運動方程式)が導かれ、経路積分全体には古典解のみが効いてくることになる。一方(3)は$[0,T]$までの間を$N$分割した各時刻で計$N-1$個の無限積分を含んでいるがこれは各時刻で粒子がどの位置$x_j$を通過するのか、$(-\infty,+\infty)$の範囲でその確率を足し合わせている(Feynman核は$0,x_0$での状態から$T,x$での状態への遷移振幅を表していることを考えると各時刻でその位置を通る確率を考えてそれを全領域で足してあげると見れる)。このような意味があって(3)式は経路積分と呼ばれる。つまりある状態からある状態まで考えられる全ての”経路”を足し上げて遷移振幅を考えるのが＜経路積分での量子力学の考え方＞であり、これは古典極限の下である古典解に帰着する。