自由な発想っていいな-Wick回転

日々思うこと

今日、ふと見たツイートの中にこんなものが。

 

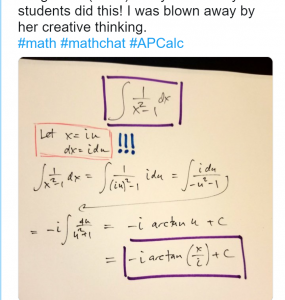
https://twitter.com/MrHonner/status/1076252469083209729

この実積分の計算を学生さんにやらせたらこの解法で解いたのだそう。

 

僕は例えば分母を部分分数分解して…っていうやり方とかをすぐに思いついたけどこれは面白い。

 

っていうのはこの考え方は”Wick回転“という数学的なテクニックに通じるものがあるから。

Wick回転というのは例えば今やりたい積分を

普通にやったら積分経路の中に特異点が含まれていて発散(=計算できなくなる)する場合、

実変数zを

z=iu   (u:実数)

のように置くことで積分範囲は実軸上(-∞,+∞)から虚軸上(-i∞,+i∞)へと移るようにさせること。

つまり

 

 

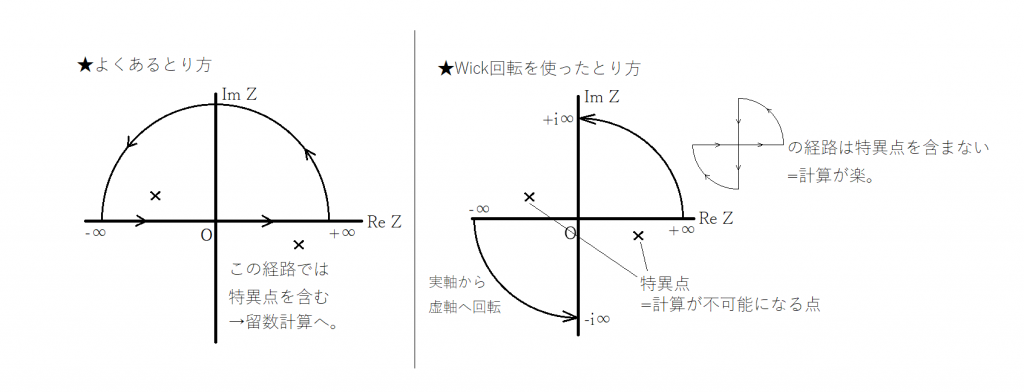
この図のように積分経路をとるようにすることで積分計算を簡単にしよう、ということである。

前者は留数を計算して…とするが、後者はCauchyの積分定理からこの積分は0とできる。

そうすることで計算が楽になるときがあるのだ。

 

今回の積分ではわざわざこんなことをしなくてもいいのかもしれないけども、発想が面白い。

最近は学校で習ったことだけを使って宿題を解きなさい、と言われ

独創的な解答がバツになったりして、それが度々話題になっている。

 

それぞれの立場があるだろうから下手なことは言えないけども、

「こうもできるな」とあれこれやってみるのは何においても楽しいだろうな、と。

 

僕は結構頭が固かったりするところもあるから、そういう発想ができる人になりたい(^^;)

僕に御言葉を教えてくださっている先生はまるでワシが空から見下ろすように

束縛されない自由な考えでいろいろなことを行なっていかれる。

自由で柔軟な発想、今日も先生から学ばないと！

Sedi

Sedi

某大学M1 摂理の物理屋。 専門は素粒子物理学 よく変人と言われます(--)

プロフィール